Evaluating a classification model is fairly straightforward and simple. You just count how many of the classifications the model got right and how many it didn't.
Evaluating a regression model is not that straightforward, at least from my perspective. One of the useful metric that is used by a majority of the implementations is R-squared.
What is R-squared?
R-squared is a goodness-of-fit test in order to evaluate how good your model fits the data. It is also known as the coefficient of determination, or the coefficient of multiple determination for multiple regression.
I know the terms might be a bit overwhelming, like the majority of statistical terms, but the explanation is quite simple. It is the percentage of variation from the mean that the model can explain. In simpler words, R-squared shows how much of the variance from the mean is explained by the model.
Consider a set of points in the target set, given by

Now, consider the set of predicted points

Let be the mean of y.
be the mean of y.
The mean variance of the data is given by,
^{2})
The explained variance by the model is given by,
^{2})
Consequently, the unexplained variance by the model is given by,
^{2})
Hence, the definition for R-squared is as follows,
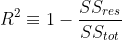
From the above equation, we can see that the value of R-squared lies between 0 and 1. 1 indicating that the model fits the data perfectly and 0 indicating that the model is unable to explain any variation from the mean. Thus we can safely assume that higher the value of R-squared, better the model is.
BUT, THIS IS NOT ENTIRELY TRUE.
Some of the scenarios where this metric cannot be used are:
Evaluating a regression model is not that straightforward, at least from my perspective. One of the useful metric that is used by a majority of the implementations is R-squared.
What is R-squared?
R-squared is a goodness-of-fit test in order to evaluate how good your model fits the data. It is also known as the coefficient of determination, or the coefficient of multiple determination for multiple regression.
I know the terms might be a bit overwhelming, like the majority of statistical terms, but the explanation is quite simple. It is the percentage of variation from the mean that the model can explain. In simpler words, R-squared shows how much of the variance from the mean is explained by the model.
Consider a set of points in the target set, given by
Now, consider the set of predicted points
Let
The mean variance of the data is given by,
The explained variance by the model is given by,
Consequently, the unexplained variance by the model is given by,
Hence, the definition for R-squared is as follows,
From the above equation, we can see that the value of R-squared lies between 0 and 1. 1 indicating that the model fits the data perfectly and 0 indicating that the model is unable to explain any variation from the mean. Thus we can safely assume that higher the value of R-squared, better the model is.
BUT, THIS IS NOT ENTIRELY TRUE.
Some of the scenarios where this metric cannot be used are:
- R-squared cannot be used as an evaluation metric for any non linear regression models. Although it might throw some light on the performance of the model, it is mathematically not a suitable metric for non linear regression. Most of the non linear regression libraries still provide R-squared as an evaluation metric for reasons unknown.
- The value of R-squared can be negative, as the model can be infinitely bad.
- As we add new variables to the linear regression model, the least squares error decreases. This leads to an increase in the R-squared value. As we can see, R-squared is an increasing function of number of variables. Hence, we cannot truly compare two models with different number of variables on this metric.
- As a corollary to the previous point, adding new variables (irrespective of their applicability to the problem) always increases. This does not necessarily mean that the model is better. In such cases, adjusted R-squared is a better metric.
No comments:
Post a Comment